"It must be nice to have summers off"

How many times have I heard this, "It must be nice to have the summers off!"

I can't believe that we still, as teachers, have to hear the same bullshit rhetoric from the very same people who entrust us to raise their kids!

You would think that I am either completely tired of hearing it and want to lose my marbles when I do OR that I've heard it so much that it no longer phases me.  I have to say that I am somewhere in the middle.  My reaction to the idea or the phrase or the ensuing conversation has changed recently and I'm not sure why.  Maybe I'm getting older and with age comes some perspective.

A couple of weeks ago I was out on a pontoon boat on one of Michigan's beautiful inland lakes drinking beer with some strangers.  They were the nicest people; 4 families who meet at the same place every year for a week in July and have been doing so for many years.

These people knew how to party.  We met them on a sandbar in this lake and they had already pulled out a long folding table and set up a beer pong game.  The competition was fierce!  Frankly the way they were "playing the wind" with their throws made me think about the physics involved in a way I shouldn't be while drinking that much beer!

I struck up a conversation with one of the 40 something adults and in true middle class fashion we asked each other what we did for a living.  I said that I was a teacher and immediately braced myself for what was coming.  Without missing a beat he said, "It must be nice..."  I use the ellipses here because I had stopped listening at that point.  Nonetheless, he went on telling me that he is an autoworker and he gets the first two weeks of July off every year and that was it for him and how jealous he was that we get like 9 straight weeks...

I didn't bother to correct him in that I was actually still working and would be for a few more weeks because his point was clear; teachers have it easy.

The most interesting part is that for those who don't know me I am quite confrontational.  With us in the conversation was an very good elementary school teacher I know and she was looking at me like,"Oh no, Don is going to blow!"  But I didn't make eye contact with her and let this guy go on with his opinions.

Why didn't I lose my shit on this guy?  Because it occurred to me recently that regardless of this guy's naive opinions of what we do or  even worse the disdain of much of the public for teachers, they still need us!  In fact, in this ever increasingly changing world, then need us more than ever!

For the past 5 years, after the school year is over, I have been running a 4 week, very intense workshop for physics teachers.  This job makes my teaching job look like a walk in the park.  I work with dedicated physics teachers and run this workshop like a physics teacher boot camp.  It is 8-4 every day for 15 straight days.  Each day is like a week of school year content and it exhausts me beyond belief.  During this time I don't get to see my wife or kids in a way that is meaningful.  But I do it because good teaching matters.

Earlier this week I was asked if I would be able to run two workshops next year.  I politely declined because my wife and I would really like to spend some time together (and with our kids) in the summer.

We sacrifice quality time during the school year knowing that we would make it up in the summer.

The educational professional who offered me the two workshops then quipped (rather passive-aggressively) "Oh, the rest of us have to work 12 months.  But you teachers..."  I let it slide because I knew he was joking but it was all I could do to NOT go through the phone and throttle him!

I know that some of your day jobs are just that, "day jobs".  That you get to leave it at work when you go home at night and on the weekends.  But when your job is raising the country's children; literally shaping the future of the nation, we, as teachers, take it very seriously and frankly need some time to regroup!  I know that every parent gets frustrated with their children - imagine dealing with 150 of them every day (or worse 25 for 8 hours each day).  Our job is serious and a couple extra weeks off in the summer is a necessary part of the job to do it effectively.

Maybe the problem is that too many of the general public aren't aware of what most teachers I know do with their summers.  Yes, we do take our kids to the pool.  And yes, we vacation.  However, many of us teach, all of us read the whole goal is to get better at the job.  I have a stack of summer reading and none of it involves vampires and all of it involves leadership.

My point is this - to the general public:  for our job raising your kids,don't you think we deserve a little extra time off just so that we can do that job effectively?

Oh and by the way - you're welcome.

Southwest Michigan Modeling Workshop Day 12

Today was a weird one.

We started the day discussing the readings - the first couple of sections of chapter 4 and an important reading by Jackson, Dukerich and Hestenes and the effectiveness of Modeling Instruction.

The Arons reading was fine but I think the participants are kind of over it.  The topic was about 2 dimensional motion and vectors.  I think at this point they understand where Arons is coming from and aren't surprised by anything he writes.  However, it is still good for them to see someone besides me talking about the importance of constructing all meaning before attempting to name it.

After the Arons article we looked at the article entitled Modeling Instruction: An Effective Model for Science Instruction.  This is the most recent article that we read in the workshop and is basically an argument about the efficacy of modeling instruction.  The participants felt that the article would be a good primmer for an administrator.  I kind of agree.  One of them felt, however, that an administrator would really need a one-page condensed version for easy digestion.  I found that kind of funny.

This article led us to a discussion of how the participants could start the year to get the administrators on their side early.  It will be hard for them to implement a whole new methodology.  It will be new and different for the kids - who may rebel a bit and if the administrators are already on their side.  

It turns out that I'm more of a big picture guy.  I see what I want to do and how I can make it happen but mostly hope that it all works out in the end through divine intervention.  I normally surround myself with those amazing detail oriented people that help me fill in the specifics, however, this summer's workshop I am flying mostly solo.

Which means that occasionally stuff falls through the cracks.  Exhibit A - when I forgot to do the free fall acceleration lab.  Oops.  We had to go back like 3 days later and fill it in.  That one was actually as much of a sequence error as an oops.

But today's oops was exactly that.  At the end of last week we were all exhausted.  We finished unit 5 and were ready to move on...or so I thought.  We never white boarded worksheet 4.  In my head last week I was thinking, "We'll just finish worksheet 4 on Monday."  But when Monday came I totally forgot and we moved on to unit 6.  It wasn't until the end of Monday that I remembered so we had to white board and discuss worksheet 4 this morning.

I was thinking that maybe we could just skip it.  Unfortunately we can't because the participants need more practice facilitating their own discussions.  Every year that we've done this the most adamant comment at a follow up session is, "I wish we'd had more practice facilitating discussions."  I wish you'd had more practice also.  However, every time we facilitate it takes like a whole hour and that is one less hour for content!  So after the reading discussions we took the rest of the morning to white board and discuss worksheet 4.

After that we jumped BACK into our discussion of energy.  Yesterday we kind of decided that we didn't have a coherent sense of energy and definitely didn't have a definition.  So today we started with listing all of the different energy types.  The participants, much like the students, came up with about 15 different types from what we expect; kinetic and elastic to some out there examples; green energy and biomass.

Probing the students here and getting on the board what is in their heads is crucial.  The point is that nothing that I'm writing down comes from me, it all comes from the students.  They are their ideas and concepts, I am just recording them.  So although it may seem like a traditional lecture set up with the teacher at the board the generation of content is upside-down.

To start to analyze their list in a physics kind of way I imposed the first rule of energy;

All energy is stored energy and you must be able to say where/how it is stored and/or how it we notice it

This rule puts students in a position to make their energy concept more concrete.  I used a bed spring and pushed it downward with a tennis ball and then let go.  The ball popped upward which begs the question, where was the energy stored?  Clearly it was in the spring - and I know that because I saw the spring compressed.  Then it was transferred to the ball and I know that because the ball is moving.  

We used this rule on our list to make sure that everything they suggested had a storage mechanism or could at least be observed as being stored.  The main reason I do this is to deal with the "potential energy problem".  For too long teachers have just called it "potential energy" without a coherent of where or how the energy is stored.  This took an intuitive leap by the participants but I suggested that it was stored in the gravitational field.  This is not awesome but is the best explanation that we have.

I introduced the idea of pie charts, did a couple of examples and then they got to work on unit 7 worksheet 1.  They white boarded the problems and we set them up to facilitate by themselves.

Long day - I hope to wrap up energy tomorrow.

Southwest Michigan Modeling Workshop Day 11

Back from a 4 day break and feeling awesome!  Although it seemed like the whole group of participants had "A case of the Mondays"!

None the less we ploughed ahead.  The problem is that there isn't any time to wait, pause or take stock.  We want to get through so much material so that the participants are armed with everything they'll need to be successful, however, real learning takes time!  So we push them harder but have to temper our pace with their learning.  Ugh, its hard.

Anyway - today we started with free fall.  We had already looked at the free acceleration (which is sometimes called free fall acceleration or acceleration due to gravity).  I drew a man on a roof dropping a ball.  The question is, we know how fast the ball is moving at each second, but how do we know how far it has fallen?

We drew a velocity vs. time graph and they shaded the area to find the displacement.  

This is not new - it is an application of the constant acceleration particle model and the participants liked the fact that it seemed to be kind of a review of something they'd seen before.  

They completed worksheet 1 as Laura and I walked around checking for understanding.

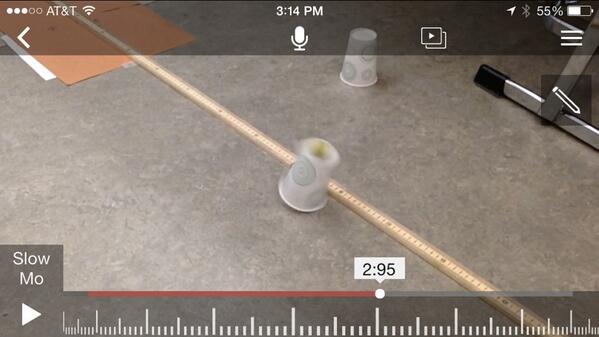
From there we did the "paradigm lab" for the projectile motion unit.  I shared with all of the participants a video of a steel ball thrown across the classroom.  

The questions is: as you watch the slow-mo version of the ball's flight, what happens to the vertical spacing of the ball's positions and what happens to the horizontal spacing of the ball's positions?  

They used an old-school overhead transparency to mark the position of the ball and then answered the questions.  It appeared that the horizontal spacing stayed constant and that the vertical spacing changed.  I asked about the forces and if this seemed consistent with what we know about the acceleration of the ball based on those forces.  

From there they jumped into worksheet 2.  As they completed it again, Laura and I walked around engaging in dialogue, asking extension questions, as always, checking for understanding.  We asked them to put a scale version of the motion map on a white board and MAN did they struggle!

But we got out of them what we wanted, deep thought about projectile motion without having to rely on the equations as a crutch.

Textbooks often put free fall and projectile motion before the forces unit.  This is, in my opinion a serious problem in that there is no reason for the motion.  Why does an object move with a constant velocity in the horizontal direction?  Why does it move with a constant acceleration in the vertical direction?  Without knowing about the forces there is no justification for the motion.  I suppose you could just observe it and go from there but why not have a complete picture?

After that we did some arts and crafts.  This wasn't my finest moment but I still think it worked out well enough.  I had them cut strings and tie them to beads so each bead hung at lengths of 5, 20, 45 and 80 cm; these are the same distances that a freely falling object falls in 1, 2, 3 and 4 seconds.  I then asked them to tape them to a meter stick at equal horizontal intervals to model constant velocity.  They were able to see how the beads modeled the parabolic motion of a horizontally shot projectile.  

I then got confused, gave bad directions, and wanted to curl up and die.

From there we did two practicum challenges.  

The first was a steel ball bearing rolling down a ramp on to a track and then off.  The goal was to hit the top of the cup on the floor.  Why the top of the cup and not into the cup?  I suppose no really good reason.  My thought was that with a heavy ball and a light cup it wouldn't go in but just tip it over.  If it hit the top then it might bounce right off!  How cool would that be?  

But frankly I don't really try to do everything perfectly in these workshops.  I occasionally fly by the seat of my pants or am purposefully vague.  Because the teachers need to figure most of this our for themselves!  I want them to say, "What was Don even doing?  This is way better if I just ________."  I hope they take this skeleton of  a structure that I've imposed and make it their own.  If they don't; if they try to imitate me they won't be as successful.  

So that is the question; how do you provide enough structure for it to make sense but not enough so that they are just following along and imitating?

The groups were quite successful with this one!

The second practicum involved a PASCO Projectile Launcher.  I launched the little yellow ball and from the table to the floor.  I then assigned each group and angle and told them they had to hit the top of the cup.

This was wicked hard!  In past workshops I've had a couple of content experts, teachers who were so good with the content (after teaching for 15 or 20 year) that nothing I threw at them was really hard.  But this group if made up of new (some super new) teachers and others that haven't ever had to teach at this level that the activity proved to be WAY hard.

But with a little coaching they were able to succeed on a level with which everyone was comfortable.  

Some groups even hit top of the cup.

This qualifies as a "really hard" physics problem and the fact that a group got it to work is amazing!

Variation and Measurement Labs

I have been Modeling – teaching physics using the Modeling Method for about 14 years now.  I took my first training in the summer of 2000 with a very dynamic teacher from Michigan, Mark Davids, who had been modeling then for at least 10 years, having received his training in 1997 and 1998.  I mention the lineage because the modeling materials have changed over time and something that I think is so important has been lost.

That is serious practice in graphing and analysis.

When I first took the class the facilitator had us to between 8 and 10 labs where we took data, graphed it (using some automatic graphing program or calculator) and analyzing the graphs - writing equations, describing the relationships, etc..  I thought that this is the way that all modelers do it.  But when I got to Arizona State (where I studied modeling for the next couple of years) I found out that no one did it this way.  They all used the script from the modeling materials that suggested doing just the pendulum lab.  

I was like, "What?  None of those are even a linear relationship!"  

How are kids going to experience all of the relationships by only doing a pendulum?  In my experience there were myriad labs with almost all of the standard relationships represented.  Here is my list of all of the labs that I have the kids do in the first week.

Linear Relationship

Circles #1: Circumference vs. Diameter

The participants measure the circumference of various cans, lids and bottles with a string and the diameter with a meter stick.

Rods: Mass vs. Length

The participants measure the length of a bunch wooden dowels cut from the same long dowel with a meter stick and the mass with a triple beam balance.

Tiles: Mass vs. Area

The participants measure the area of pieces of white board with 1 cm x 1 cm grid paper and the mass with a triple beam balance.  I cut a white board into small pieces of various sizes and shapes between 50 cmxcm and 500 cmxcm.

Spheres: Mass vs. Volume

The particpants measure the volume of 5 differnt steel ball bearings by dropping them into a graduated cylinder and the mass with a triple beam balance.

Cups and Dice:  Mass vs. Number of Dice

The participants count the number of dice in a cup and measure the total mass with a triple beam balance.  This one is particularly interesting!

Parabolic or Quadratic or Squared Relationship

Circles #2: Area vs. Diameter

The participants measure the area of circles with 1 cm x 1 cm grid paper and measure the diameter with a meter stick.

Square Root Relationship

Pendulum #1: Period vs. Length

The participants measure the period of the pendulum with a stop watch and the length using a meter stick.

No Relationship or No Variation

Pendulum #2: Period vs. Mass 

The participants measure the period of the pendulum with a stop watch and the mass by reading the mass on some "physics class masses".

Pendulum #3: Period vs. Angle

The participants measure the period of the pendulum with a stop watch and the angle by using a protractor or other "angle-o-meter".

Inverse Variation

Baseball Balance: Distance to Center vs. Mass

The participants vary the mass on one end of a meter stick and change the distance from the center by sliding it toward or away getting it to balance.   

There isn't an inverse square relationship here but that doesn't mean I can't do one.  

I am tired of teachers who say, "these kids don't have any skills."  I am like, "then just teach them what you want them to know!"  

With in these labs I teach my kids how to measure with meter sticks, stop watches and balances.  They learn to make white boards, to graph with the computer and to analyze their graphs; all of the skills they will need for the whole year!  And I am in the room coaching and watching and hinting.  I get to know the kids and their skill level.  

I have been running Modeling Workshops in Michigan for 5 years now and have done these with my participants and I bet if you ask any of them they will support my claim that these are valuable parts of their classes.

Southwest Michigan Modeling Workshop Day 10

Two-thirds of the way through the workshop and I am exhilarated and exhausted!

On day 10 we had some very challenging physics questions to tackle.  The first involved a box on a ramp (what we physics people call an inclined plane problem).  The second involved the Atwood's Machine - and half or modified Atwood's Machine (what we physics people call a two-body-problem).  

The day started with a discussion of the readings from Arons.  The reading was about the common vocabulary of physics with regard to "gravity".  In our modeling class we don't use the word "gravity" at all; in fact I call it the "g-word" and don't let anyone use it!  There are much better ways to refer to things kids usually call "gravity" and Arons goes into detail in this section.
I couldn't agree more with Arons and we talked all about our own conceptions and his observations.

We then embarked on the ramp problems.  After 4 years of leading a workshop (and 15 years of teaching) I still don't have a great way to get students or teachers to discover or construct on their own how to draw a force diagram for a box on a ramp.  It is very frustrating.  So I, instead, wanted to see if I could somehow link what we were doing to this new process.

Earlier in the workshop we had referenced a section of the Arons reading where he suggested a flashlight demo to help students resolve vectors into their component parts.  Take a meter stick to represent a vector and lean it against a wall.  How would you know how long to make the horizontal and vertical components.  Arons says to take a flash light and shine it parallel to the floor and on the wall you'll see the vertical component.  Then take the flash light and shine it perpendicular to the floor and you'll see the horizontal component.

Our participant have really embraced this idea and have even gone to calling the components the "shadow arrows".  

So the question is how does one draw the component vectors for a box on a ramp?  Traditionally we were told to just "rotate the axis" and then break up the weight vector into its component parts.   But this instruction was given without a reason or context.  It was, "just the way you do it".   So I practiced and got good at it but never really knew why.  And I want at least a little more for the participants.

We decided to use the idea of the flashlight demo to link this new problem to something we already understand.  The rule is:

To find the components shine the flash light parallel and then perpendicular to the surface.

This rule gives us a reason to "rotate the axis".  Since the flash light is orientated according to the surface even if we tilt the surface we can still find the shadow arrows!  Moreover, these arrows have to be, themselves, parallel and perpendicular to that surface.

In the end the participants still had to practice.  But I am more comfortable giving them a little more than this is  "just the way you do it".

Unfortunately I had to show them how to do it, which isn't the end of the world.  I don't mind doing an "on the board" demonstration if it is a particular skill I want them to master.  While finishing, one of the participants asked, "how do you convince the students the angle of the ramp is the inside angle of the component triangle?"  

I was like, "I try never to show them anything they can figure out on their own!"  So I asked them to use the method I just described and then measure the two angles and see for themselves.  

The engineering group above used a bit of technology (my favorite app called "clinometer") so measure the two angles.  Other groups used protractors or those giant Plexiglas triangles from geometry class.  The point is, nobody is confused about the fact that those two angles are the same.  No geometry necessary; convincing needed!

Then they practiced.  This basically took all morning.  Ugh.  Learning is so slow when it is meaningful.  

We then moved onto the dreaded Atwood's Machine problems.  These again are tough for almost all physics students.  Why?  It is hard to say.  Probably because you have to think about two objects instead of just one.  But is that really that much harder?

Apparently so.  As teachers we need to practice our RETROGRADE AMNESIA; remembering back to a time when you didn't know or know how to do something.  

Do you remember back to when you didn't know how to tie your shoes? Do you think you could effectively and easily teach that skill to someone without remembering what that feels like? It is the same with these problems!

The issue, again, is traditionally we were told how to do these and just practiced until we got it right.  This involved drawing a force diagram for each object and then writing a sum of the forces statement for each. This would yield two equations and two unknowns. Then from there we do some math-magic (also known as algebra) and solve for something; the tension in the string or the acceleration. Kind of tough for all but the best students (who are probably just following the procedure without thinking too much about it anyway).

Can we do better? What kind of construct can we apply to this problem that is a bridge between what we already know and this new situation?

We decided to go for a system approach for the modified Atwood's Machine. We started by drawing a force diagram for each body and then asking the question, "What is the role of the pulley?" I suggested that it was to turn the force 90 degrees. What would the force diagram look like if we undid the pulley? Can we then smush the force diagrams together to find the unbalanced force?

We asserted that Newton's 2nd Law applied to systems as well:

a(sys) = Funbal(sys) / m(sys)

Once we had the unbalanced force and mass for the system we could then find the acceleration of the system. This procedure allows us to simplify the large problem into something manageable. The participants, however, had to make that cognitive leap in order to get on board with this idea.

Not too many had a problem and we made sure to work with them and that they had enough practice.

The day ended with a practicum challenge.  They were given a Modified Atwood's Machine and asked to release it and a buggy at the same time so that the little mass on the end of the string landed in the buggy.  The group that was the closest landed it on the hood.

I didn't assign any homework because it was the 4th of July weekend.

Mass - do we even know what it is?

Today in class we talked about a reading from chapter 3 in the Arons book.  He asked the differences between gravitational mass and inertial mass.  The participants were like, "Forget the differences, what ARE gravitational and inertial mass?"  I was like, "forget gravitational and inertial, WHAT IS MASS?"  Do we have an operational definition for mass?

No, really, do we have an operational definition for mass?  In all of the years that I've been teaching I never have come up with anything that made sense.  We have an idea of mass (at least we can say if an object has more mass than another) and even measure it in kilograms.  But what it is?

I've had to rely on the circular reasoning argument that "all matter is made of atoms and has mass" and then "mass is the amount of matter contained in an object".   These statements, unfortunately, make so sense at all!  We still don't have a good definition of mass.  WTF!

To make matters worse it turns out that we have no way to directly measure the mass of an object!  I asked in class and they suggested a balance - but that is a comparison between an already known mass based on a gravitational force; how did you establish the first mass?  Then they suggested the "inertial balance" which puts you in a position to measure the frequency of a vibrating mass and inferring the value for the mass.  Someone suggested we just push with a force and measure the acceleration; again inferring the mass.

We don't have a way to measure the mass of an object!  I am not sure that the participants have thought that deeply about mass as a concept before but we still have a long way to go with it.

I am thinking about an operation definition that allows us to use the mass but doesn't hinge on a origin.  How about this:

mass is the measurement of an object's resistance to change in motion

We know that the natural tendency of an object is to resist changes in its motion; an object at rest will tend to stay at rest and an object in motion will tend to stay in motion (in a straight line at a constant speed).  But which will resist changes more, a basketball or a bowling ball?  Obviously the bowling ball, but do we know why?  It is not because it weighs more - we're not trying to pick it up.    Its because it has more mass!  

The more mass the more resistant to changes in its motion.  We measure this in kilograms which is quite arbitrary but we've decided to go with it.  

I can't wait to see how the participants respond to this idea.

Southwest Michigan Modeling Workshop Day 9

Started the day with white boards from acceleration, mass and force lab which is ostensibly the Newton's 2nd Law lab.  Yesterday they had made white boards where each group varied two quantities of the four:
1.  Pulling force
2.  Mass of the cart
3.  Angle of the pull
4.  Angle of the ramp

We looked at the boards and found out that there was a linear relationship between pulling force and acceleration.  In addition there was an inverse relationship between mass and acceleration.  These were the two expected results and they came out quite good despite the trepidation of the groups about the wonky lab procedures.  They didn't think that pushing or pulling the cart with a spring scale would give good enough data to model the actual physical laws.

But the data came out great - WHAT'S UP NOW!  To be honest, this isn't my first rodeo!  This was enough to move on to generate the law, but we still had two more situations to examine.

Next came the pull angle.  We looked at their data and my question was - if you break up the pulling force into it's "shadow arrows" the component forces, which one is responsible for the acceleration.  AND which one is the unbalanced force?  We looked at a couple of the situations and it turned out that the horizontal component was the unbalanced force and responsible for the acceleration.  In addition, it changes with the angle.  So we looked at a couple of situations (30 and 60 degrees) and asked the questions how does the unbalanced force change and how does the acceleration change?

I was very specific here to make note of the unbalanced force which I called the Funbal.  The participants immediately started calling it the FunBall; which I love!  This is WAY better than Fnet or Sum of the Forces because it ground the understanding in the language.

I decided to ignore the angle of the ramp.  Mostly because we didn't yet have any context in which to analyze the forces of a cart on a hill.  More on that tomorrow.

Once we got to the point of seeing that the the pull force and the mass were the only real factors that affected the acceleration we used the mathematical structure of those relationships to create one equation that related all three variables:

a = (coefficient)Funbal/mass

The participants then set up their stations to solve for the coefficient.  With the exception of one group (who ti think had faulty equipment) each group found a coefficient very close to 1.0 and we settled on that and wrote the law.  

From there we talked about what the Funbal meant in a few different situations and I set them on unit 5 worksheet 1 the elevator problems.  They worked on these but had significantly more difficulty that I thought they would.  That, however, is very positive.  It means that they were either in a very good "student mode" or that they need the content help.  Both work for me.

This is kind of where the wheels fell off the cart. One of the questions asks what would happen if the elevator cable broke.  At that moment I realized that we never measured a free fall acceleration.  This is because in my class I don't do things in the prescriptive modeling order and I would have done free fall before this.  But I forgot!  So we went back and talked about what happened to the acceleration of the cart when you increased the angle of the ramp.  And it its max angle do we know the acceleration?

They set up the situation and measured the free acceleration of various objects, a book, a ball, anything they could drop.  Asked them to get the acceleration after a drop AND after an object was thrown upward a little bit.  They found and white boarded this data and we agreed upon a free acceleration of 10 m/s/s.

Then I asked them to ride the elevator and find the 4 accelerations.  One group used a bathroom scale, one group put a 5 N mass on a spring scale.  Two groups used data taken with LabQuests.

We then asked them to find the acceleration of the elevator using their actual data.
This was a little challenging but worth the effort.

I then asked then to relate the force diagrams, the acceleration of the rider to how you feel (heavy light or normal).

The point of the discussion is that:

Our bodies are not speedometers - they are accelerometers!

When they finished that activity we decided to finally talk about the readings.  The first reading was from Hake and was on the SDI labs that he ran at IU.  The participants liked the dialogue and felt that it well reflected what Laura and I are trying to do in the class.  I tried to emphasize that we are not promoting the SDI labs but highlighting the importance of the Socratic Dialogue in the classroom.

I have an idea that in order to create the constructivist science classroom you need two aspects:
1.  Inquiry lab experiences
2.  Socratic Dialogues

Neither one by itself will lead to the promised land, but together they can be very powerful!

The second reading we talked about was from Arons.  He asked the differences between gravitational mass and inertial mass.  The participants were like, "Forget the differences, what ARE gravitational and inertial mass?"  I was like, "forget gravitational and inertial, WHAT IS MASS?"  Do we have an operational definition for mass?

No, really, do we have an operational definition for mass?  In all of the years that I've been teaching I never have come up with anything that made sense.  We have an idea of mass (at least we can say if an object has more mass than another) and even measure it in kilograms.  But what it is?

I've had to rely on the circular reasoning argument that "all matter is made of atoms and has mass" and then "mass is the amount of matter contained in an object".   These statements, unfortunately, make so sense at all!  We still don't have a good definition of mass.  WTF!



To make matters worse it turns out that we have no way to directly measure the mass of an object!  I asked in class and they suggested a balance - but that is a comparison between an already known mass based on a gravitational force; how did you establish the first mass?  Then they suggested the "inertial balance" which puts you in a position to measure the frequency of a vibrating mass and inferring the value for the mass.  Someone suggested we just push with a force and measure the acceleration; again inferring the mass.

We don't have a way to measure the mass of an object!  I am not sure that the participants have thought that deeply about mass as a concept before but we still have a long way to go with it.